My first semester here I elected to take a geohydrology course. Since most of my experience lies in the geophysical methods. I wanted to learn more about water and how it moves through the earth. This class was an excellent course because it exposed me to basic foundation in groundwater modeling. I think the most interesting thing is that the resistivity equation and the groundwater flow equation are almost identical. The groundwater modeling is a little more difficult because of the source and sink term that is usually ignored in resistivity.
Basic Theory
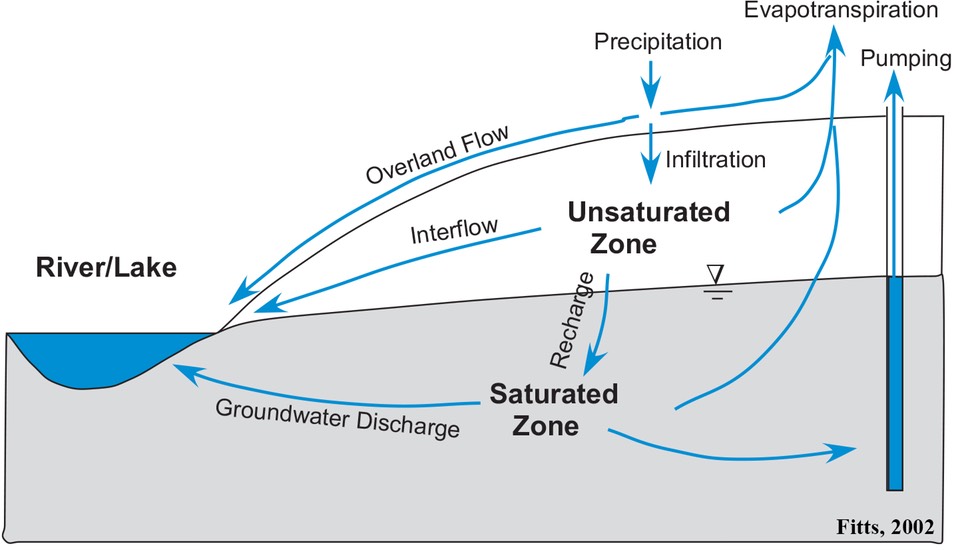
The image above was copied out “Groundwater Science”, written by Charles Fitts in 2002. This image was key in helping me learn to communicate to the hydrologists. As a geophysicist I really had no idea how some of these key regions were quantified and measured. I am hoping to focus my research in the unsaturated zone or near the interface of the unsaturated and saturated zone. I am particularly interested how these groundwater aquifers recharge in crystalline environments. I would like to start to exploring different ways to image different zones and processes that this this cartoon illustrates.
Key Equations
Below are lists of important equations that I learned throughout the course. These equations are key to understanding how hydrologists measure and quantify groundwater properties. The first one is Bernoulli’s equation. This equation defines the hydraulic head at a well location. For the scope of this class we always assumed a static condition, or a condition in which v was very small and neglected from this equation.
The next equation is probably one of the most important equations in groundwater modeling and hydrology. This equation is known as Darcy’s Law. Essentially it describes the discharge or flow rate through a material with a known hydraulic conductivity. This law is only valid when the flow is laminar, which is a decent approximation for slowly moving groundwater. The equation below is Darcy’s Law for a homogeneous distribution of hydraulic conductivity.
The last important equation that was pulled out of this class was the 3D ground water flow equation. In summary the ground water flow equation is derived by balancing the Darcy flux through a unit volume. When the flow is at steady state the flow equation represents Laplace equation.
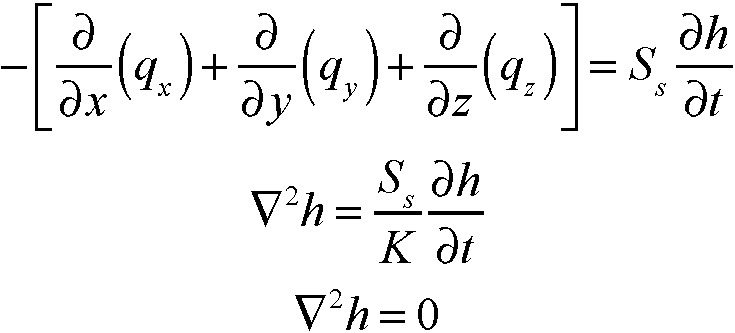
The top equation is the general 3D form, where Ss is the storativity term. The second equation down assumes that Kx, Ky and Kz do not vary with space. The third equation assume steady state flow, i.e. the flow in and out of a unit volume is equal. This equation is common and is called Laplace’s equation and I have solved this numerically in my numerical differential equations course (link coming soon).