I took this course in the fall semester of 2013. This was an extremely intellectually engaging course, because it gave me a fundamental understanding of seismic waves through the earth, and a much greater understanding of tensor analysis and elastic properties. Along with all of the gained knowledge I wrote a lot of code to illustrate some of these basic principles.
The Wave Equation
A solution to the 1D wave equations, illustrated as waves on a string. In the first plot each color has slightly different parameters, the red has the slowest velocity and widest pulse width, where the blue solution has the highest velocity and narrowest pulse width. The solution was solved by summing 600 normal modes in the Fourier domain.
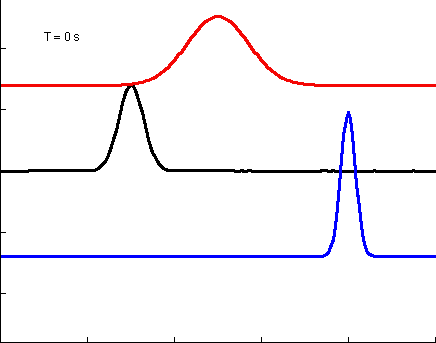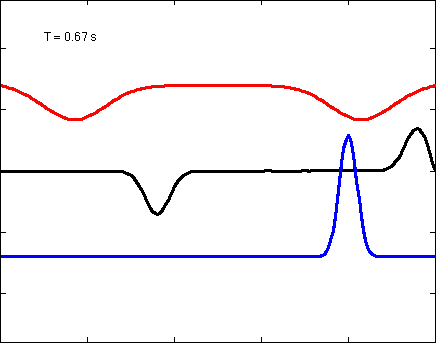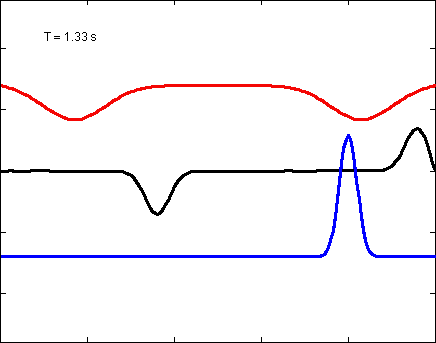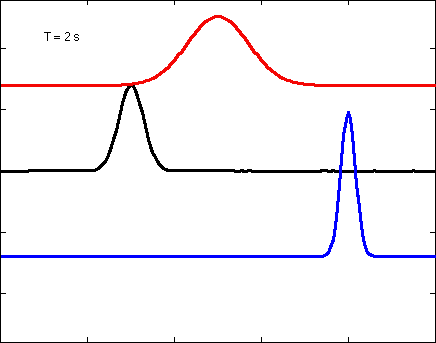
Solution to 1D wave equation on a string.
A solution to the 2D wave equation that is illustrated by a moving plane wave in 3-dimensional space. This particular wave has is traveling diagonally in the x, y plane.
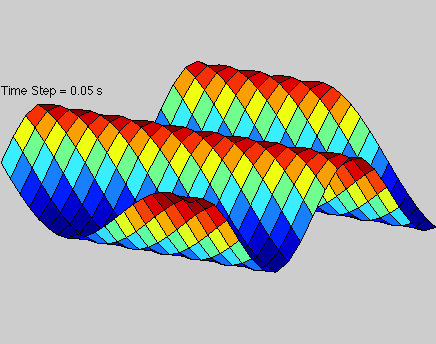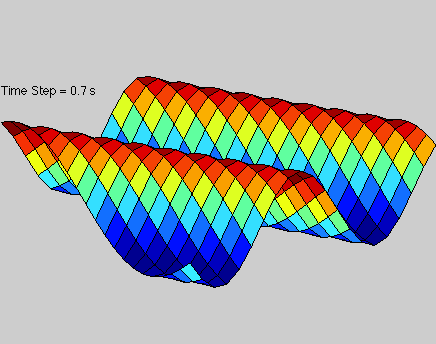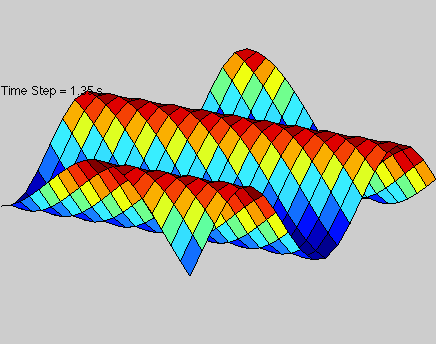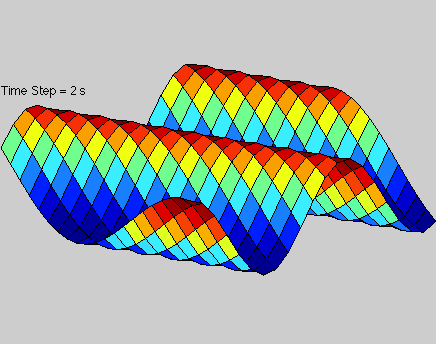
Solution to 2D wave equation in space.
Rayleigh Waves and Dispersion
Something that I found interesting and valuable to my near-surface geophysics research, is a much better understanding of Rayleigh waves. Since I will be using Rayleigh waves to calculate shear velocities in the upper 30 meters I am very glad I under stand their motion and the equations that govern them!

A small movie that shows what happens to particles in the subsurface as a Rayleigh wave passes through them. A Rayleigh waves results when the s-wave and p-wave travel harmonically at the free-surface!
We looked at dispersion curves of Rayleigh waves and calculated their group velocities. Although this is from a passive seismology point of view, we do nearly the same process when we try to pick the dispersion curves to invert for s-wave velocities. It's really nice to know how to do this myself, using zero-phase filters and envelope functions. Note the lower frequencies travel faster than the higher frequencies!
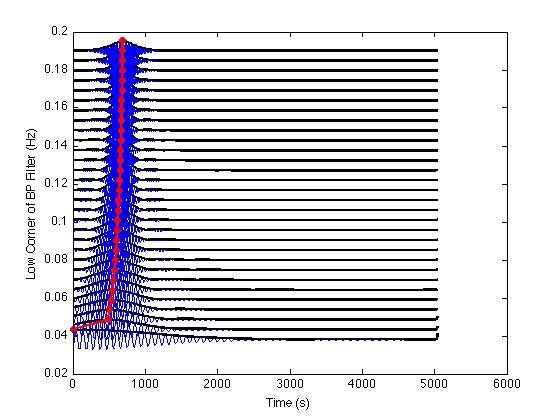
The figure above shows a Rayleigh wave that has been filtered with small zero-phase band pass filters (low end of BP filter on y-axis). If you know how far away this station was from the earthquake your one step away from calculating the group velocity!
Group vs Phase Velocity
Probably, one of my favorite parts of this course was that the definitions of phase and group velocities FINALLY clicked in my head. Whenever you have two or more waves of different frequencies traveling together you can get a phase or group velocity. The phase velocity does not transmit any energy, only the group velocity does. The very simple case to illustrate this is shown below:
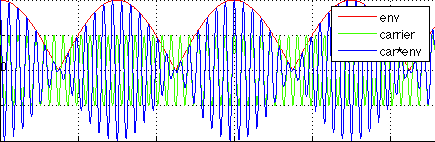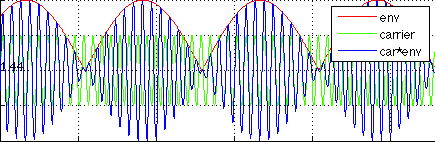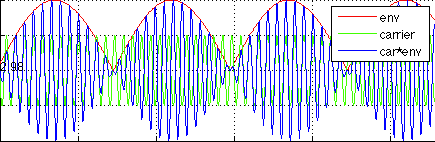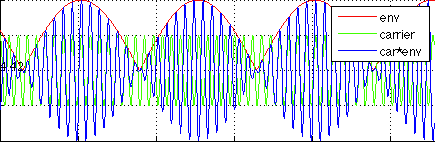
The addition of two waves traveling at different speeds and at different frequencies result is a wave moving in the right hand direction (group velocity) and the phase velocities moving in the opposite direction.